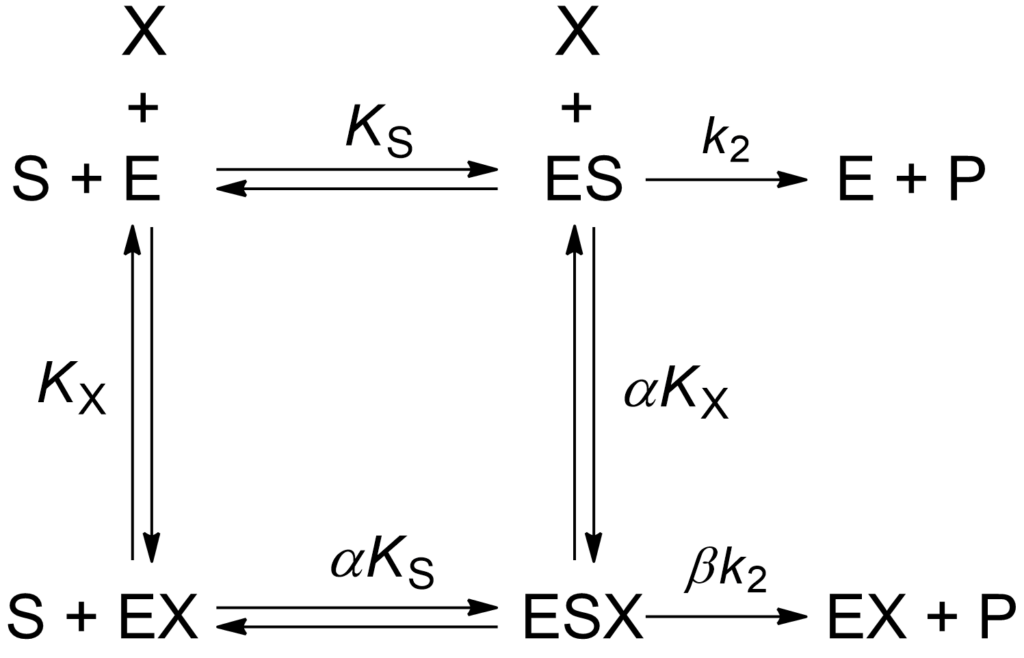
The General Modifier Mechanism: Scheme and rate equation

 (1)    \begin{equation*} \ratev = \dfrac{{{k_2}\left( {1 + \beta \dfrac{{\left[ {\rm{X}} \right]}}{{\alpha {K_{\rm{X}}}}}} \right){{\left[ {\rm{E}} \right]}_{\rm{t}}}\left[ {\rm{S}} \right]}}{{{K_{\rm{m}}}\left( {1 + \dfrac{{\left[ {\rm{X}} \right]}}{{{K_{\rm{X}}}}}} \right) + \left[ {\rm{S}} \right]\left( {1 + \dfrac{{\left[ {\rm{X}} \right]}}{{\alpha {K_{\rm{X}}}}}} \right)}}\ \end{equation*}

The symbols in square brackets represent the concentrations of total enzyme [E]t, free substrate [S] and free modifier [X], and Km is the Michaelis constant. The equation is valid under the equilibrium assumption, whose terms of validity have been discussed [Baici (2015), Chapter 2]. Even if the equilibrium or the quasi-equilibrium assumptions are not valid, the expected deviations from the complete model based on the steady-state rate equation are masked by experimental errors, with the exception of extreme cases.

Reference

Baici A (2015) Kinetics of Enzyme-Modifier Interactions – Selected Topics in the Theory and Diagnosis of Inhibition and Activation Mechanisms. Springer, Vienna