An experimental issue

In the absence of explicit symbolism, the reactant  concentrations that appear in the rate equations, e.g. [S] or [X], represent the concentrations of the free species assuming no appreciable sequestration of the considered molecules by the enzyme, i.e. [S] ≈ [S]_t and [X] ≈ [X]_t, where t means total. If velocity measurements are performed at comparable concentrations of enzyme (E) and modifier (X) and these concentrations fall in the range of the dissociation constant of the EX complex (K_X), a non-negligible portion of modifier is bound to the enzyme thus invalidating the condition [X] ≈ [X]_t.

Therefore, tight-binding of modifiers to enzymes is merely an experimental issue that in some cases can be circumvented by appropriate experiment design. When this is not possible, a dedicated equation (1) overcomes this problem and allows calculating accurate kinetic parameters.

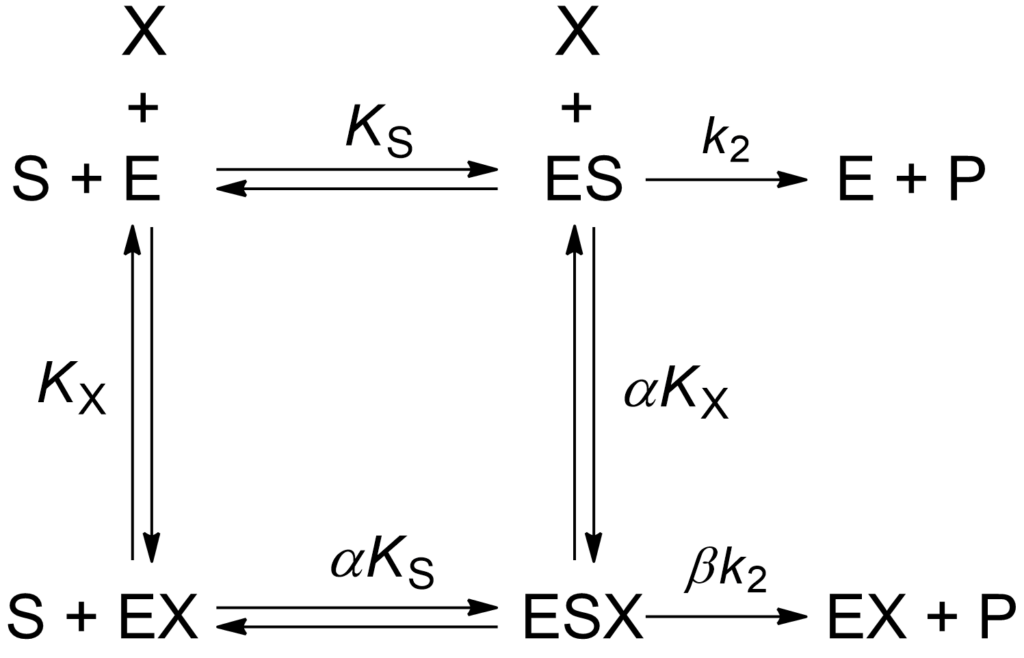
The story of this equation and its derivation can be found in [1, pp. 183-185 and 204-206). Here we go straight to discuss its application. Equation (1) is written using the same symbols found in other equations in this website, the general modifier mechanism, reproduced here as Scheme 1, and the specific velocity equation.

The discussion in The final polish explained that fitting the complete rate equation of the general modifier mechanism to data without any constraint  can be a very difficult task. This problem is even more important when fitting (1) to data. Thus, before attempting this analysis, the underlying mechanism should be identified, e.g. using the specific velocity plot, from which  the values of α and β can be calculated and constrained in the successive step.  Since the Michaelis constant is known from experiments in the absence of modifier, σ can be calculated as [S]/K_m and constrained as well. If the titrated enzyme active site concentration [E]_t is known, also  this value can be constrained thus allowing trustful fitting of (1) to data. However, if the active site concentration of the enzyme cannot be measured, [E]_t can be considered as an unknown concentration to be determined by nonlinear regression fitting.

The procedure will now be illustrated with a real case, the inhibition of human caspase-2 by a designed ankyrin repeat protein [2]. Since a titrating substance was not available, the enzyme concentration was measured photometrically. K_m for the substrate Acetyl-Val-Asp-Val-Ala-Asp-7-amino-4-methylcoumarylamide was 55.3 μM. In the presence of the modifier, the ankyrin repeat AR_F8, pilot measurements suggested that inhibition of caspase-2 was a rapid process and that the interaction was relatively tight. Therefore, the inhibition mechanism was investigated in two steps starting from the identification of the basic modifier mechanism using the specific velocity plot. This revealed a hyperbolic mixed, predominantly specific inhibition mechanism with α = 2.9 ± 0.8 and β = 0.04 ± 0.01.

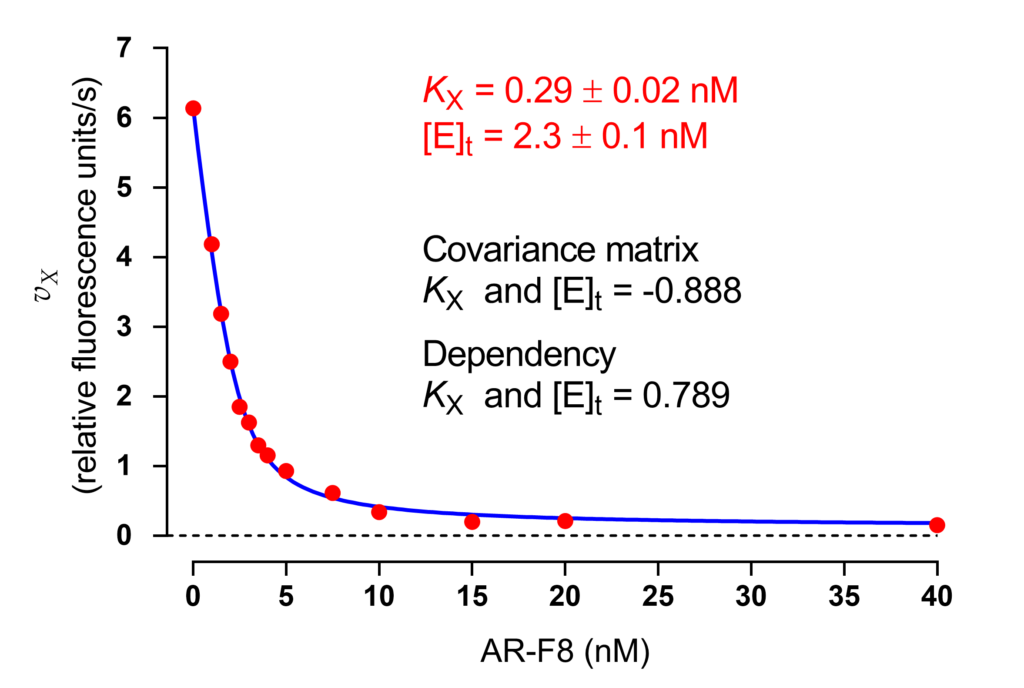
Instead of considering several combinations of substrate and inhibitor concentrations, a single titration curve was then measured at fixed [S] = 40 μM and 13 inhibitor concentrations plus the rate in the absence of inhibitor (Fig. 1). The final polishing step was performed by fitting the tight-binding equation (1) to data with constraints α = 2.9, β = 0.04, and σ = [S]/K_m = 0.72.

The sole unknowns in (1) were K_X and [E]_t. Their best-fit values are shown in the inset of Fig. 1 together with the covariance matrix and the dependency of K_X and [E]_t. The enzyme concentration in the assay was about 1 nM as total  protein measured photometrically. Caspase-2 is a dimer of two identical subunits and thus the value of [E]_t determined by regression analysis agrees with a stoichiometry of one AR_F8 molecule bound to each  subunit.