In essential activation, the involved enzymes are completely inactive in the presence of their substrates unless a further substance, typically a metal ion or a small molecule, is present. A short introduction of the classification of essential activation mechanisms is given below, while more details, including the derivation of rate equations and the criteria for mechanism discrimination, can be found elsewhere [1, pp. 142-153]. Unless the properties of the essential activator are the target of a study at various reactant concentrations, the activator (X) is usually added to assays at a fixed concentration and any interaction with other modifiers can be studied as described in the accompanying section. Therefore, essential activation will not be discussed further in this website.
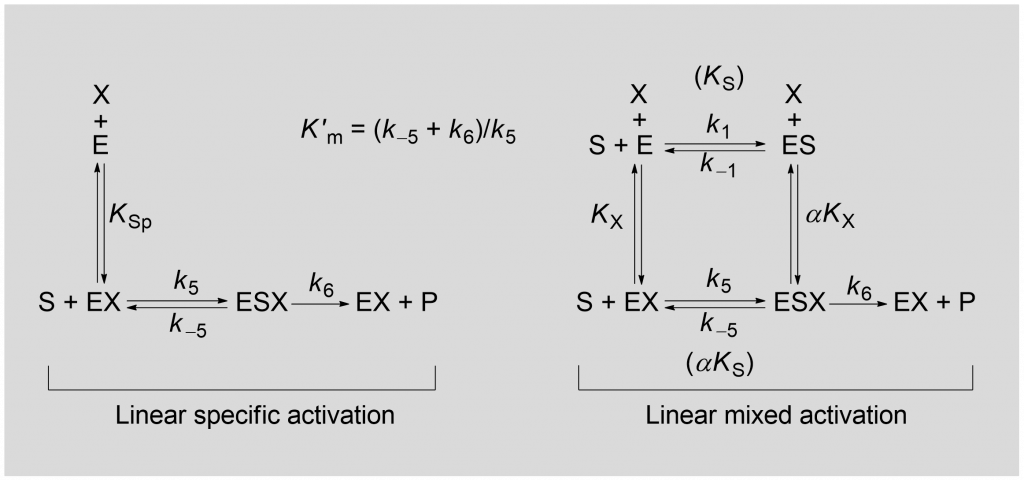
With only four members, the mechanisms of essential activation are less numerous that those in the group of inhibitors and nonessential activators. Scheme 2 shows the reactions involved in linear specific activation and linear mixed activation, where X is the essential activator [1, Chapter 3].
This taxonomic group (Fig. 2) is independent of that of the inhibitors and nonessential activators. In line with the inhibitor counterparts, though redundant, the adjective linear is part of the names of these mechanisms because their identification at a glance from the acronym or from the full name is the goal of this nomenclature.
Linear specific activation can be formally derived from the reaction paths of linear mixed activation by setting αKX = 0. Linear mixed activation (yellow-boxed in Fig. 2) consists of three mechanisms that depend on the differentiating character, α. Since in essential activation there is only one catalytic branch, there are no further mechanisms as descendants.
With reference to Scheme 2, two relevant equations can be derived under the quasi-equilibrium assumption [1, Chapter 3]: the rate equation for linear specific activation, eq. (1) and that for linear mixed activation, eq. (2).
(1) ![Rendered by QuickLaTeX.com \begin{equation*} \ratev = \dfrac{{{k_6}{{\left[ {\rm{E}} \right]}_{\rm{t}}}\left[ {\rm{S}} \right]}}{{K_{\rm{m}}^\prime\left( {1 + \dfrac{{{K_{{\rm{Sp}}}}}}{{\left[ {\rm{X}} \right]}}} \right) + \left[ {\rm{S}} \right]}} \end{equation*}](https://www.enzyme-modifier.ch/wp-content/ql-cache/quicklatex.com-bd831aa611ed1d9904f2e8fa8e058fed_l3.png)
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \ratev = \dfrac{{\dfrac{{{k_6}}}{{1 + \dfrac{{\alpha {K_{\rm{X}}}}}{{\left[ {\rm{X}} \right]}}}}\left[ {\rm{S}} \right]{{\left[ {\rm{E}} \right]}_{\rm{t}}}}}{{K_{\rm{m}}^\prime \times \dfrac{{1 + \dfrac{{{K_{\rm{X}}}}}{{\left[ {\rm{X}} \right]}}}}{{1 + \dfrac{{\alpha {K_{\rm{X}}}}}{{\left[ {\rm{X}} \right]}}}} + \left[ {\rm{S}} \right]}} \end{equation*}](https://www.enzyme-modifier.ch/wp-content/ql-cache/quicklatex.com-0ff3039511aaf1c22bc20c3ea74b8af9_l3.png)
With the definitions in Scheme 2, in the equations above:
(3) 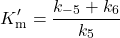
With the appropriate values of α, eq. (2) applies to the three linear mixed mechanisms in Fig. 2.
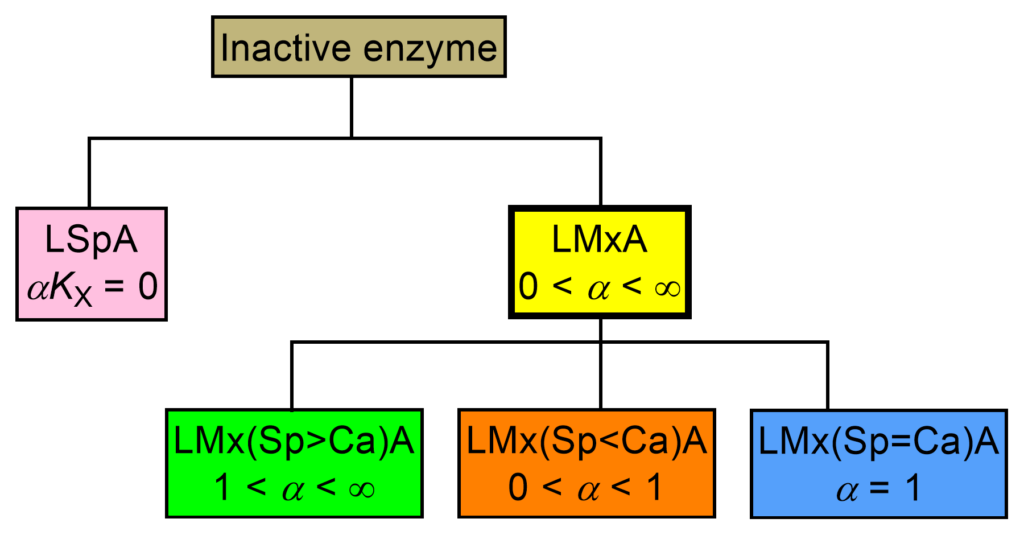
| ACRONYM | NAME |
|---|---|
| LSpA | Linear specific activation |
| LMx(Sp>Ca)A | Linear mixed, predominantly specific activation |
| LMx(Sp<Ca)A | Linear mixed, predominantly catalytic activation |
| LMx(Sp=Ca)A | Linear mixed, balanced activation |
If the properties of an essential activator in the presence of another modifier (inhibitor or nonessential activator) are the target of a kinetic investigation, the methods devised for multiple enzyme-modifier interactions can be used as detailed elsewhere [1, Chapters 6, 7].
Download PDF: Systematics of enzyme-modifier mechanisms
Reference
- Baici A (2015) Kinetics of Enzyme-Modifier Interactions – Selected Topics in the Theory and Diagnosis of Inhibition and Activation Mechanisms. Springer, Vienna