K-systems and V-systems
A popular subdivision of the mechanism by which enzymes interact with modifiers has been introduced by Monod, Wyman and Changeux [1]. This classification is based on how the modifier affects Km and V as follows:
K-systems (K-type): those in which the modifier exerts an effect on the apparent affinity of the substrate for the enzyme, and conversely
- K-inhibition (Km ↑): Kmapp increases for increasing [X]
- K-activation (Km ↓): Kmapp decreases for increasing [X]
V-systems (V-type): those in which the modifier exerts an effect on the apparent limiting rate, and consequently on kcat
- V-inhibition (V ↓): V app decreases for increasing [X]
- V-activation (V ↑): V app increases for increasing [X]
However, reporting results only as K-type activation and V-type inhibition, or as K-type inhibition and V-type activation may be ambiguous unless other properties are specified. Table 1 shows that disambiguation is necessary for the six hyperbolic mechanisms highlighted in red. In fact, there is no chance of further subdivision if, besides V (or kcat) and Km, also the dependencies of 1/kcat , kcat/Km and optionally also Km/kcat on [X] are considered as explained below.
In defense of the K– and V-system subdivision, all papers that applied it consistently and provided suitable graphical documentation of the experiments to allow readers to guess the missing details, do not leave doubts about the nature of the enzyme-modifier interactions described.
The kinetic parameters depend on [X]
The method for extracting kcat and Km from experiments was explained in the section Raw data, where also the derived parameters 1/kcat , kcat/Km and Km/kcat were discussed. As shown in Fig. 1, all five parameters can
- be independent of [X] (A, D, H, L, O)
- increase hyperbolically when [X] increases (B, E, I, M, P)
- decrease hyperbolically when [X] increases (C, F, J, N, Q)
Additionally, 1/kcat , Km and Km/kcat can
- increase linearly when [X] increases (G, K, R)
Each inhibition or activation mechanism is characterized by a unique sequence of five out of the eighteen elements in Fig. 1. The kinetically meaningful combinations must be built by inspection of the equations of the parameters taking into account the physically possible values assumed by α and β shown in the taxonomic tree of mechanisms (Fig. 2). The equations below are shown in the same color as their dependencies on [X] in Fig. 1.
(1) ![Rendered by QuickLaTeX.com \begin{equation*} \textcolor{red}{k_{{\rm{cat}}}^{{\rm{app}}} = {k_2} \times \dfrac{{1 + \beta \dfrac{{\left[ {\rm{X}} \right]}}{{\alpha {K_{\rm{X}}}}}}}{{1 + \dfrac{{\left[ {\rm{X}} \right]}}{{\alpha {K_{\rm{X}}}}}}},\quad \quad \dfrac{1}{{k_{{\rm{cat}}}^{{\rm{app}}}}} = \dfrac{1}{{{k_2}}} \times \dfrac{{1 + \dfrac{{\left[ {\rm{X}} \right]}}{{\alpha {K_{\rm{X}}}}}}}{{1 + \beta \dfrac{{\left[ {\rm{X}} \right]}}{{\alpha {K_{\rm{X}}}}}}}}\\ \end{equation*}](https://www.enzyme-modifier.ch/wp-content/ql-cache/quicklatex.com-88e21fd9c6198b7fc79b6fce32da9d77_l3.png)
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \textcolor{blue}{K_{\rm{m}}^{{\rm{app}}} = {K_{\rm{m}}} \times \dfrac{{1 + \dfrac{{\left[ {\rm{X}} \right]}}{{{K_{\rm{X}}}}}}}{{1 + \dfrac{{\left[ {\rm{X}} \right]}}{{\alpha {K_{\rm{X}}}}}}}}\ \end{equation*}](https://www.enzyme-modifier.ch/wp-content/ql-cache/quicklatex.com-dde14faa5279ff032809e4b37776c434_l3.png)
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \textcolor{OliveGreen}{{\left( {\dfrac{{{k_{{\rm{cat}}}}}}{{{K_{\rm{m}}}}}} \right)^{{\rm{app}}}} = \dfrac{{{k_2}}}{{{K_{\rm{m}}}}} \times \dfrac{{1 + \beta \dfrac{{\left[ {\rm{X}} \right]}}{{\alpha {K_{\rm{X}}}}}}}{{1 + \dfrac{{\left[ {\rm{X}} \right]}}{{{K_{\rm{X}}}}}}}}\ \end{equation*}](https://www.enzyme-modifier.ch/wp-content/ql-cache/quicklatex.com-0959ef5fe4ed89ccf554fca65536f941_l3.png)
(4) ![Rendered by QuickLaTeX.com \begin{equation*} \textcolor{OliveGreen}{{\left( {\dfrac{{{K_{\rm{m}}}}}{{{k_{{\rm{cat}}}}}}} \right)^{{\rm{app}}}} = \dfrac{{{K_{\rm{m}}}}}{{{k_2}}} \times \dfrac{{1 + \dfrac{{\left[ {\rm{X}} \right]}}{{{K_{\rm{X}}}}}}}{{1 + \beta \dfrac{{\left[ {\rm{X}} \right]}}{{\alpha {K_{\rm{X}}}}}}}}\ \end{equation*}](https://www.enzyme-modifier.ch/wp-content/ql-cache/quicklatex.com-63573903b8acc2ad9f05e57ecfe79378_l3.png)
As a stimulating exercise guess the shape of the plots that characterize the seventeen basic modifier mechanisms using the information in Fig. 2 and the colored equations above. Otherwise, trust the information in Table 2.
Put the theory in practice with your data
This website offers a validation facility for determining the mechanisms of enzyme-modifier interactions with just a few mouse clicks (recommended). However, again as exercise, you can also do this by hand as described below.
- Perform the primary data analysis discussed in Raw data
- Calculate the apparent kcat, Km, 1/kcat, kcat/Km, and Km/kcat for each modifier concentration and plot the results against [X]
- To identify the mechanism it is not necessary to perform any fitting of equations to data: just inspect the points and deduce whether they describe a hyperbola or a straight line
- Check if the hyperbolas increase or decrease with increasing [X] and compare your results with the shapes in Fig. 1
- Write down the 5-letter code and check it against the codes in Table 2 to identify the mechanism
It can be argued if all five dependencies of the parameters on [X] listed in Table 2 are necessary for the identification of a mechanism. For instance, this is not the case of linear specific inhibition, which is unambiguously identified from the linear dependence of Kmapp on [X]. The reason for looking also at the dependencies of the other parameters is that the nature of the enzyme-modifier interaction in a new system under investigation is still unknown and, in the presence of experimental error, looking at the five dependencies can be very useful.
With this information at hand, preliminary values of the parameters can be calculated, so that one/two of them can be constrained for the FINAL POLISH.
Table 1. Subdivision of K-systems and V-systems according to Monod et al. [1] and comparison with the subdivision of hyperbolic mechanisms described in this website. The six mechanisms shown in red cannot be distinguished from one another using only K-type and V-type definitions.
| K-type | V-type | Mechanisms | |
|---|---|---|---|
| activation (Km ↓) | and | activation (V ↑) | HMx(Sp<Ca)A |
activation (Km ↓) | and | inhibition (V ↓) | HCaI HMx(Sp<Ca)I HMxD(A/I) |
inhibition (Km ↑) | and | activation (V ↑) | HMxD(I/A) HCaA HMx(Sp>Ca)A |
| inhibition (Km ↑) | and | inhibition (V ↓) | HMx(Sp>Ca)I |
| inhibition (Km ↑) | only | − | HSpI |
| − | only | inhibition (V ↓) | HMx(Sp=Ca)I |
| activation (Km ↓) | only | − | HSpA |
| − | only | activation (V ↑) | HMx(Sp=Ca)A |
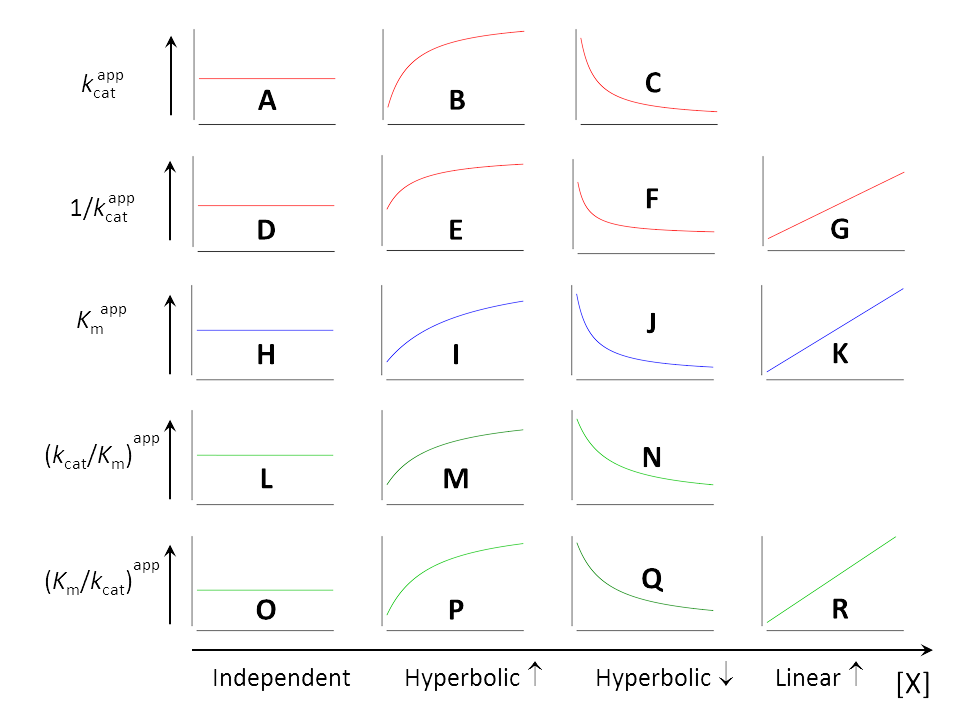

Table 2. The letter codes, taken from Fig. 1, that characterize the dependencies of the kinetic parameters on modifier concentration for the seventeen basic modifier mechanisms. The codes are unique, and if the plots are evaluated in sequence left-to-right as in the heading row, the five letters of each code are in alphabetical order.
| Mechanism | kcat | 1/kcat | Km | kcat/Km | Km/kcat | Code |
| LSpI | A | D | K | N | R | A D K N R |
| LCaI | C | G | J | L | O | C G J L O |
| LMx(Sp>Ca)I | C | G | I | N | R | C G I N R |
| LMx(Sp<Ca)I | C | G | J | N | R | C G J N R |
| LMx(Sp=Ca)I | C | G | H | N | R | C G H N R |
| HSpI | A | D | I | N | P | A D I N P |
| HCaI | C | E | J | L | O | C E J L O |
| HMx(Sp>Ca)I | C | E | I | N | P | C E I N P |
| HMx(Sp<Ca)I | C | E | J | N | P | C E J N P |
| HMx(Sp=Ca)I | C | E | H | N | P | C E H N P |
| HMxD/(I/A) | B | F | I | N | P | B F I N P |
| HCaA | B | F | I | L | O | B F I L O |
| HMx(Sp>Ca)A | B | F | I | M | Q | B F I M Q |
| HMxD(A/I) | C | E | J | M | Q | C E J M Q |
| HSpA | A | D | J | M | Q | A D J M Q |
| HMx(Sp<Ca)A | B | F | J | M | Q | B F J M Q |
| HMx(Sp=Ca)A | B | F | H | M | Q | B F H M Q |
Download PDF: Mechanisms from parameters
Download PDF: Dependencies of the kinetic parameters on modifier concentration
References
- Monod J, Wyman J, Changeux JP (1965) On the nature of allosteric transitions: a plausible model. J Mol Biol 12: 88-118. doi:10.1016/S0022-2836(65)80285-6
- Baici A (2015) Kinetics of Enzyme-Modifier Interactions – Selected Topics in the Theory and Diagnosis of Inhibition and Activation Mechanisms. Springer, Vienna