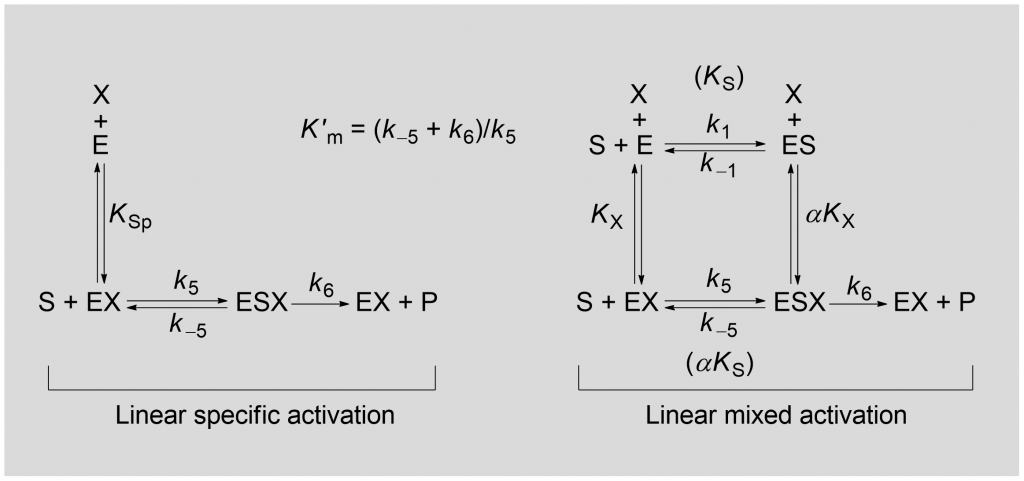
With only four members, the mechanisms of essential activation are less numerous that those in the group of inhibitors and nonessential activators. Scheme 2 shows the reactions involved in linear specific activation and linear mixed activation, where X is the essential activator [1, Chapter 3].

This taxonomic group (Fig. 2) is independent of that of the inhibitors and nonessential activators. In line with the inhibitor counterparts, though redundant, the adjective linear  is part of the names of these mechanisms because their identification at a glance from the acronym or from the full name is the goal of this nomenclature.

Linear specific activation can be formally derived from the reaction paths of linear mixed activation by setting αK_X = 0. Linear mixed activation (yellow-boxed in Fig. 2) consists of three mechanisms that depend on the differentiating character, α. Since in essential activation there is only one catalytic branch, there are no further mechanisms as descendants.

---

With reference to Scheme 2, two relevant equations can be derived under the quasi-equilibrium assumption [1, Chapter 3]: the rate equation for linear specific activation, eq. (1) and that for linear mixed activation, eq. (2).

 (1)    

 (2)    

With the definitions in Scheme 2, in the equations above:

 (3)    

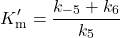
With the appropriate values of α, eq. (2) applies to the three linear mixed mechanisms in Fig. 2.

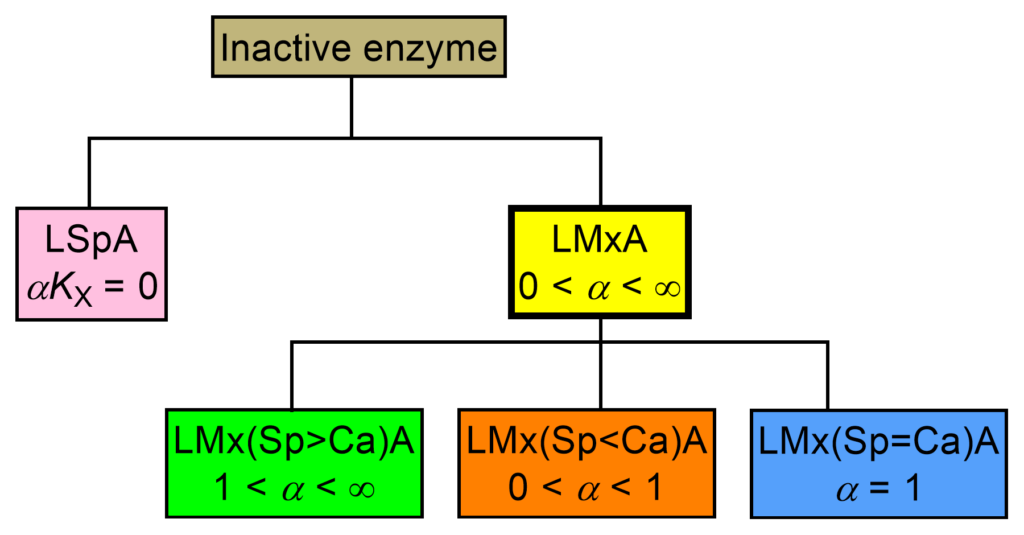
ACRONYM	NAME
LSpA	Linear specific activation
LMx(Sp>Ca)A	Linear mixed, predominantly specific activation
LMx(Sp<Ca)A	Linear mixed, predominantly catalytic activation
LMx(Sp=Ca)A	Linear mixed, balanced activation

If the properties of an essential activator in the presence of another modifier (inhibitor or nonessential activator) are the target of a kinetic investigation, the methods devised for multiple enzyme-modifier interactions can be used as detailed elsewhere [1, Chapters 6, 7].