Mixed inhibition as defined here encompasses such a broad range of behaviour that it may sometimes be helpful to subdivide it further .
Nomenclature Committee of the International Union of Biochemistry (1982). Symbolism and terminology in enzyme kinetics. Recommendations 1981
Eur. J. Biochem. 128, 281–291 (p. 287) Electronic version
Systematics of inhibition and nonessential activation
The model considered in the systematization of kinetic modifier mechanisms presented here is the general modifier mechanism published in 1953 by Jean Botts and her husband Manuel Francisco Morales [1] (Scheme 1). The detailed description of the underlying theories can be found elsewhere [2, Chapters 2 and 3], where also the reasons for choosing the adjectives specific in place of competitive, and catalytic in place of uncompetitive are explained. Balanced applies to mechanisms in which the specific and the catalytic components are equally represented.
In the notation of the general modifier mechanism shown in Scheme 1 (left) the specific and the catalytic components of the reaction are highlighted with colors. KSp and KCa represent the dissociation constants of the specific and of the catalytic branch, respectively. The notation on the right of the scheme is more practical for writing rate equations and the dissociation constants KX and αKX refer to both inhibitors and activators. α is the reciprocal allosteric coupling constant, and β is the factor by which the modifier affects the catalytic constant k2.
The taxonomy of enzyme-modifier mechanisms is based on the two characters α and β of the general modifier mechanism, where α is the dominant character. There are 17 basic mechanisms by which enzymes interact with inhibitors and nonessential activators. In the taxonomic tree of modifier mechanisms (Fig. 1) these are treated as species and ranking starts at the root on the top of the dendrogram as unmodified, active enzyme.
In Fig. 1, linear specific inhibition (LSpI, the same as competitive inhibition), and linear catalytic inhibition (LCaI, the same as uncompetitive inhibition) are considered primordial species without progeny, while linear mixed inhibition (LMxI, yellow-boxed) is the ancestor of the remaining fifteen mechanisms.
- The lineage with a green background has a specific or a predominantly specific character (1 < α < ∞)
- The lineage with an orange background has a catalytic or a predominantly catalytic character (0 < α < 1)
- In the lineage with a blue background the specific and the catalytic characters are equally represented (balanced, α = 1)
Within the three lineages, the secondary character β and its relationships with the primary character α establish when inhibition or activation occurs.
Proceeding from the root towards the bottom through levels 1-3, the mechanisms become more sophisticated in fine-tuning enzyme activity by either inhibition, activation or both in the same context. Therefore, the dendrogram in Fig. 1 represents the evolution from an ancestor to descendants, but just metaphorically, without phylogenetic pretenses, since the tree is based exclusively on phenetic, experimentally observable present-day characters.
With appropriate values of α and β, the rate equation of the general modifier mechanism (eq. 1) describes all mechanisms in Fig. 1:
(1) ![Rendered by QuickLaTeX.com \begin{equation*} \ratev = \dfrac{{{k_2}\left( {1 + \beta \dfrac{{\left[ {\rm{X}} \right]}}{{\alpha {K_{\rm{X}}}}}} \right){{\left[ {\rm{E}} \right]}_{\rm{t}}}\left[ {\rm{S}} \right]}}{{{K_{\rm{m}}}\left( {1 + \dfrac{{\left[ {\rm{X}} \right]}}{{{K_{\rm{X}}}}}} \right) + \left[ {\rm{S}} \right]\left( {1 + \dfrac{{\left[ {\rm{X}} \right]}}{{\alpha {K_{\rm{X}}}}}} \right)}}\ \end{equation*}](https://www.enzyme-modifier.ch/wp-content/ql-cache/quicklatex.com-f57a276e9b244e9bda47a9b61b74cc8b_l3.png)
In (1) the symbols in square brackets represent the concentrations of total enzyme [E]t, free substrate [S] and free modifier [X], and Km is the Michaelis constant. Equation (1) is valid under the equilibrium assumption, whose terms of validity have been discussed [2, Chapter 2]. Even if the equilibrium or the quasi-equilibrium assumptions are not valid, the expected deviations from the complete model based on the steady-state rate equation are masked by experimental errors, with the exception of extreme cases.
Definition of linear and hyperbolic enzyme modification
The definitions are based on the shape of the plots of the reciprocal catalytic constant (1/kcat) and of the reciprocal specificity constant (Km/kcat) against [X], the modifier concentration. Both plots can be linear or hyperbolic, or at least one is either linear or hyperbolic when the other parameter is independent of [X].
- Inhibition is said to be linear when at least one of the 1/kcat or Km/kcat plots against [X] is a straight line
- Inhibition and nonessential activation are hyperbolic when at least one of the 1/kcat or Km/kcat plots against [X] is a hyperbola (nonessential activation is in any case always hyperbolic)
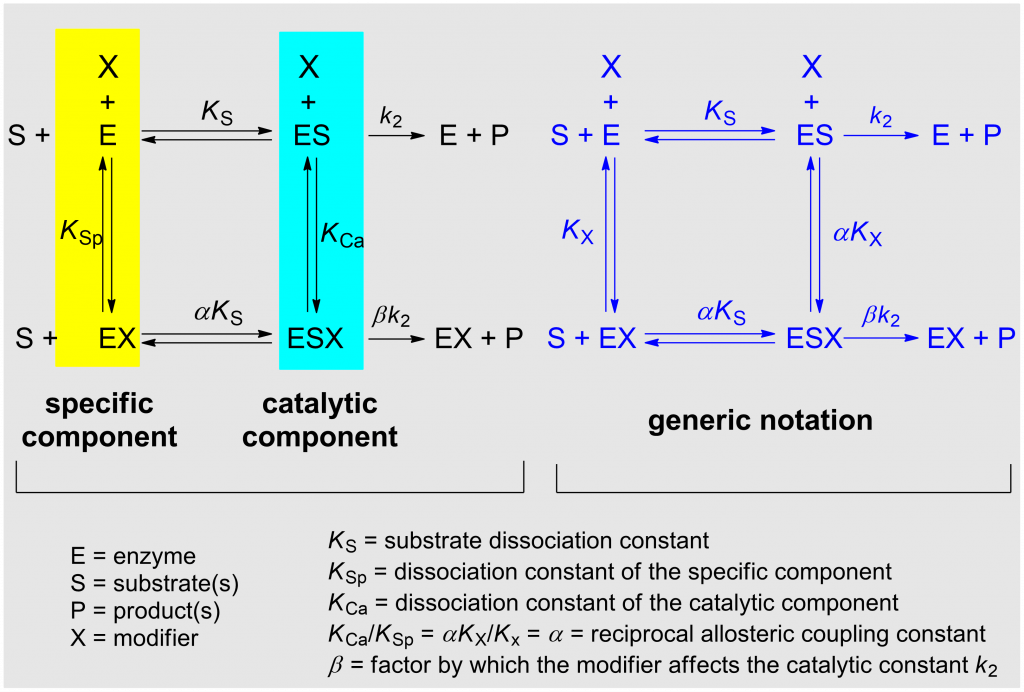
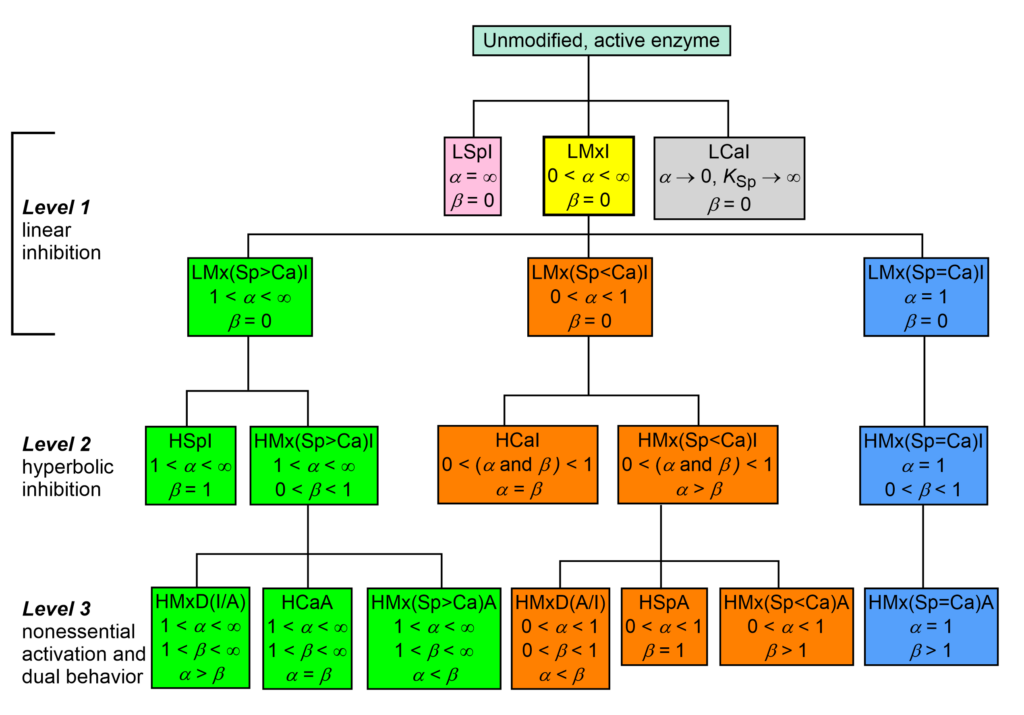
Fig. 1. Taxonomy of enzyme-modifier interactions. Zoom/Download
The acronyms in Fig. 1 are composed of the following elements:
A = activation, Ca = catalytic
D = dual, inhibition or activation, depending on substrate concentration
H = hyperbolic, I = inhibition, L = linear, Mx = mixed, Sp = specific
(Sp>Ca) = predominantly specific, (Sp<Ca) = predominantly catalytic
(Sp=Ca) = balanced, i.e. the specific and catalytic components are equally represented
| ACRONYM | NAME |
|---|---|
| LSpI | Linear specific inhibition |
| LCaI | Linear catalytic inhibition |
| LMx(Sp>Ca)I | Linear mixed, predominantly specific inhibition |
| LMx(Sp<Ca)I | Linear mixed, predominantly catalytic inhibition |
| LMx(Sp=Ca)I | Linear mixed, balanced inhibition |
| HSpI | Hyperbolic specific inhibition |
| HCaI | Hyperbolic catalytic inhibition |
| HMx(Sp>Ca)I | Hyperbolic mixed, predominantly specific inhibition |
| HMx(Sp<Ca)I | Hyperbolic mixed, predominantly catalytic inhibition |
| HMx(Sp=Ca)I | Hyperbolic mixed, balanced inhibition |
| HMxD(I/A) | Hyperbolic mixed, dual modification (inhibition → activation) |
| HCaA | Hyperbolic catalytic activation |
| HMx(Sp>Ca)A | Hyperbolic mixed, predominantly specific activation |
| HMxD(A/I) | Hyperbolic mixed, dual modification (activation → inhibition) |
| HSpA | Hyperbolic specific activation |
| HMx(Sp<Ca)A | Hyperbolic mixed, predominantly catalytic activation |
| HMx(Sp=Ca)A | Hyperbolic mixed, balanced activation |
The names assigned the mechanisms are logical and are formed using terms suggested in the IUB-Recommendations 1981. The reasons for choosing terms that may not yet be familiar to readers, have been discussed in reference [2, Chapter 3]. Specific (suggested in the Recommendations) in place of competitive and catalytic, in place of uncompetitive (not suggested in the Recommendations) have been used by Cárdenas and Cornish-Bowden [3]. Two new terms had to be created: balanced in place of the deprecated noncompetitive, and dual for mechanisms that display inhibition or activation depending on substrate concentration.
Download the systematics of enzyme-modifier interactions
References
- Botts J, Morales M (1953) Analytical description of the effects of modifiers and of enzyme multivalency upon the steady state catalyzed reaction rate. Trans Faraday Soc 49: 696-707
- Baici A (2015) Kinetics of Enzyme-Modifier Interactions – Selected Topics in the Theory and Diagnosis of Inhibition and Activation Mechanisms. Springer, Vienna
- Cárdenas ML, Cornish-Bowden A (1989) Characteristics necessary for an interconvertible enzyme cascade to generate a highly sensitive response to an effector. Biochem J 257: 339-345.